How Experimentation handles outliers

Overview

This topic explains how LaunchDarkly Experimentation handles outliers in its experiment analyses.

An outlier is a data point that has a value much higher or much lower than the other points in its data set. Outliers are typically caused by unusual or illogical behavior from someone included in an experiment. If handled incorrectly, an outlier can negatively impact your experiment results by skewing the analysis and making it more difficult to make informed decisions.

For example, imagine you are running an experiment comparing sales revenue for a product when you offer a 10% discount, versus when you offer no discount. Most people buy just one or two of your product at a time, so it's easy to compare sales volume between the discounted and non-discounted treatments. Now imagine that a customer buys 1,500 of your product at full price to distribute to students at the school they work for. This data point is now an outlier, as it is very unusual customer behavior. If not handled correctly, the outlier could make it seem like the full-price variation of your product was more popular than the discounted variation, when this wasn't true for most customers.

Experimentation outlier handling

LaunchDarkly Experimentation handles outliers using Bayesian statistics' built-in handling method. The method uses an experiment's control variation to create strong priors. This means that, for every experiment, LaunchDarkly includes prior beliefs about your data gathered from the control variation to formulate an expected range of outcomes. This expected range of outcomes is called the posterior distribution. Because LaunchDarkly uses real end-user behavior to create these posterior distributions, the distributions have a small credible interval with low variance. Therefore, any outliers in the variations you're experimenting on do not have a strong effect on the distribution.

To learn more about prior beliefs in Bayesian statistics, read Frequentist and Bayesian modeling.

This is an example of a narrow posterior distribution:

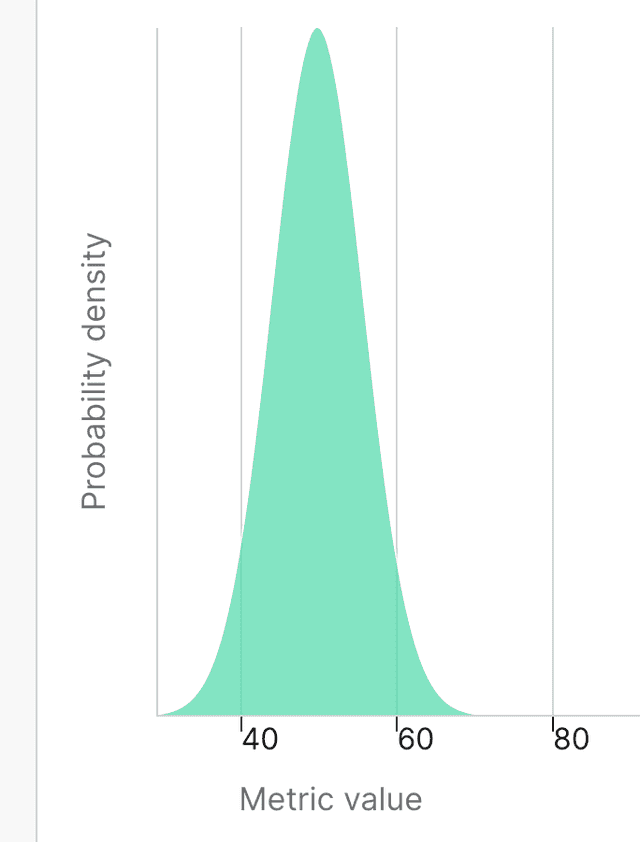
The narrow curve means the variation has a small credible interval, giving you high confidence in your prior beliefs and a low risk of data skew due to outliers. To learn more, read about credible intervals.